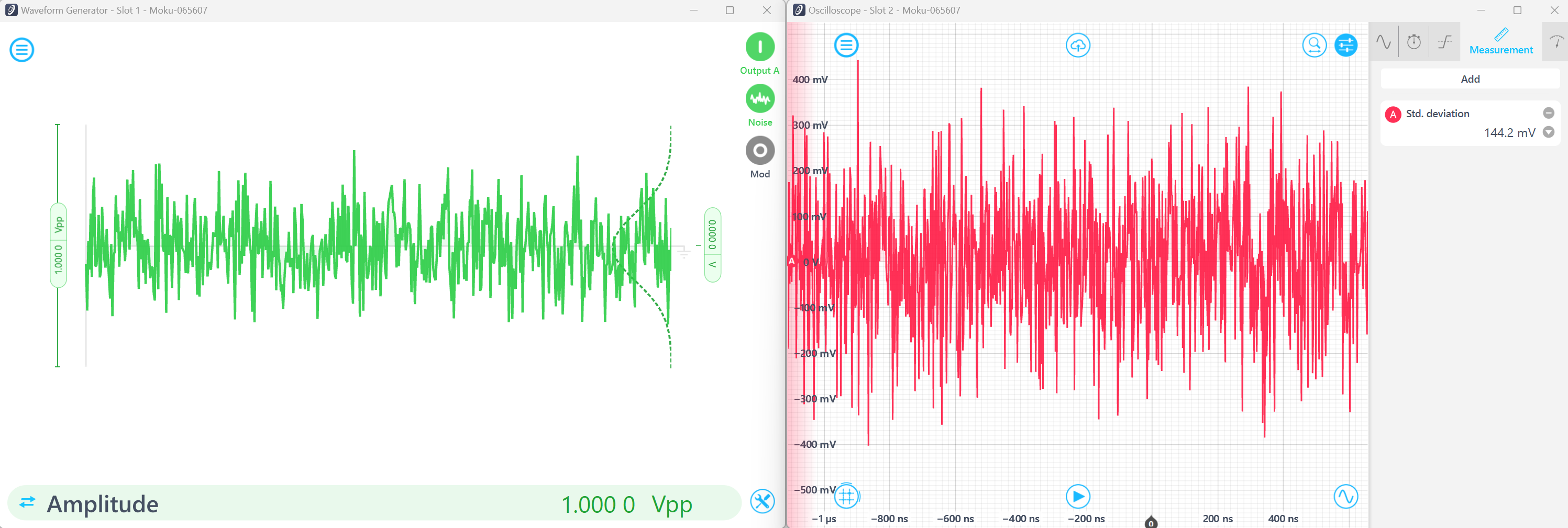
Moku波形ジェネレーター: ノイズ振幅とは何を意味しますか?
Moku波形ジェネレータはノイズを生成できる
- Moku:Lab
- Moku:Go
-
Moku:Pro
Moku:Proに関するよくある質問 Moku:Pro波形発生器 Moku:Proタイム&周波数アナライザ Moku:Proロジックアナライザ/パターンジェネレーター Moku:Proレレーザーロックボックス Moku:Proロックインアンプ Moku:Proスペクトラムアナライザ Moku:Proデータロガー Moku:Pro任意波形発生器 Moku:Proマルチ機器モード Moku:Pro位相計 Moku:Pro FIRフィルタービルダー Moku:Pro PIDコントローラー Moku:Proオシロスコープ Moku:Pro周波数応答アナライザ Moku:Proデジタルフィルターボックス
- Python API
- MATLAB API
- 任意波形発生器
- データロガー
- デジタルフィルターボックス
- FIR フィルタ ビルダー
- 周波数応答アナライザー
- レーザーロックボックス
- ロックインアンプ
- オシロスコープ
- 位相計
- PIDコントローラー
- スペクトラムアナライザー
- 時間と周波数アナライザー
- 波形発生器
- ロジックアナライザ/パターンジェネレーター
- マルチ機器モード
- Mokuクラウドコンパイル
- Mokuに関するよくある質問
- LabVIEW API
理想的なガウスノイズは理論上は範囲が無制限で、振幅は無限大まで拡張できますが、極端に大きな値になる確率は極めて低くなります。ただし、実際には、すべてのデバイスの出力範囲に固有の制限があるため、電子ノイズ信号発生器で真のガウス分布ノイズを生成することはほぼ不可能です。したがって、ガウス分布ノイズに近似するノイズ発生器を実装する必要があります。
一様分布の乱数を生成するのは簡単で、FPGA システムで簡単に実装できます。たとえば、線形フィードバック シフト レジスタ (LFSR) は、一様分布の疑似乱数を生成するために広く使用されているアルゴリズムです。ただし、ガウス分布のノイズを実現するには、一様分布をガウス分布に変換する必要があります。
2 つの一様分布を加算すると、それらの分布の畳み込みが行われます。時間領域でランダム変数を加算することは、ランダム変数の確率密度関数で畳み込みを実行することと同じです。詳細については、このリンクを参照してください。
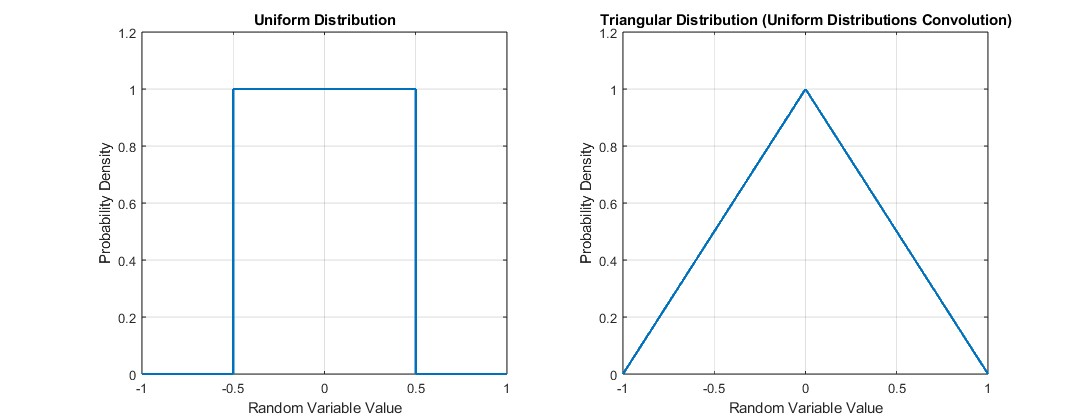
2 つの一様分布を畳み込むと、三角分布が生成されます。
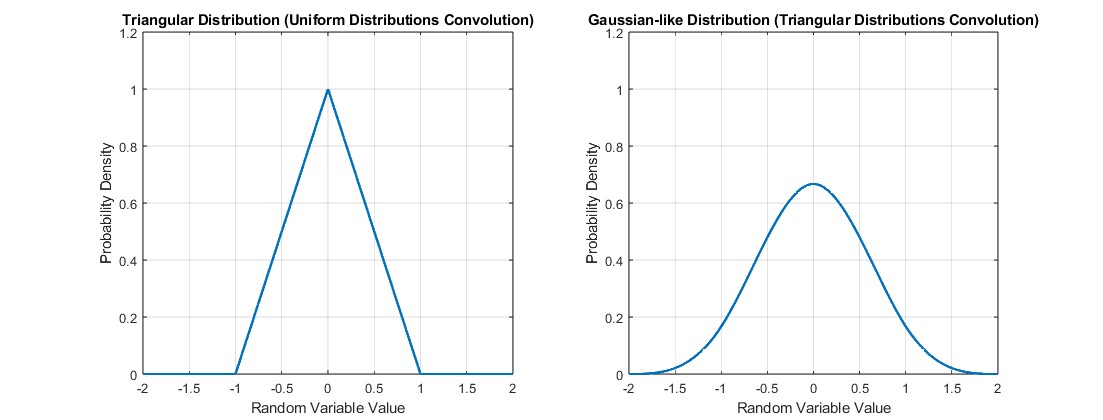
2 つの三角分布を畳み込むと、ガウス分布のような分布が得られます。
σ = sqrt(1/48) の真のガウス分布が生成され、再スケールされたガウスのような分布と比較されています。ガウスのような分布は真のガウス分布にかなり近似していることがわかります。
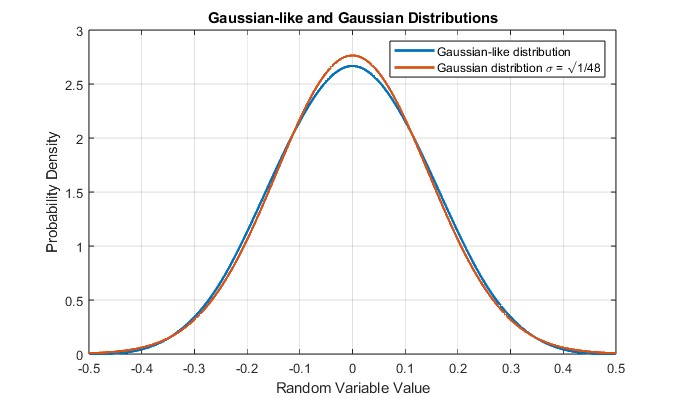
一定範囲の一様分布の分散 は1/12です。4つの独立した一様分布のランダム変数を追加すると、分散が 4/12。しかし、この新しい変数の範囲は から 。1の範囲を維持するために、この変数は4分の1に縮小する必要があります。その結果、再スケーリングされたランダム変数の分散は1/48ですしたがって、再スケーリングされたランダム変数の標準偏差はsqrt(1/48)です
たとえば、 Moku波形ジェネレータが 1 Vpp のノイズ波形を出力する場合、信号の最小値と最大値はそれぞれ -0.5 V と 0.5 V です。1 Vpp のノイズ信号の標準偏差は約 144.338 mV で、これは sqrt(1/48) です。