ロックイン アンプは、ノイズの多い環境での小信号解析に広く使用されている機器です。ロックイン アンプには、X/Y や R/θ など、いくつかの出力モードがあります。ただし、ロックイン アンプ内の処理チェーンが複雑なため、入力信号の振幅と R 出力の間に直接的な関係はありません。

入力信号が単一の周波数トーンで構成される特定のケースでは、入力信号をその周波数で復調すると、出力信号の振幅を直接決定できます。

1. シングルトーン入力信号:

同じ周波数fで復調された、 A ⋅ sin(f ⋅ t)という形式の入力信号を考えます。ミキサーの出力は、 A ⋅ sin(f ⋅ t) ⋅ sin(f ⋅ t)です。倍角の公式を使用すると、この信号は[1 - cos(2f ⋅ t)] ⋅ A/2と表すことができます。成分2f はローパス フィルターによってフィルター処理され、 A/2が残ります。したがって、出力 R は信号振幅Aの半分、ピークツーピーク振幅値の 4 分の 1 になります。

実験結果によりこの関係が確認されています。500 mVpp 振幅信号を持つ 1 MHz 信号の場合、復調結果 R は 125 mV です。

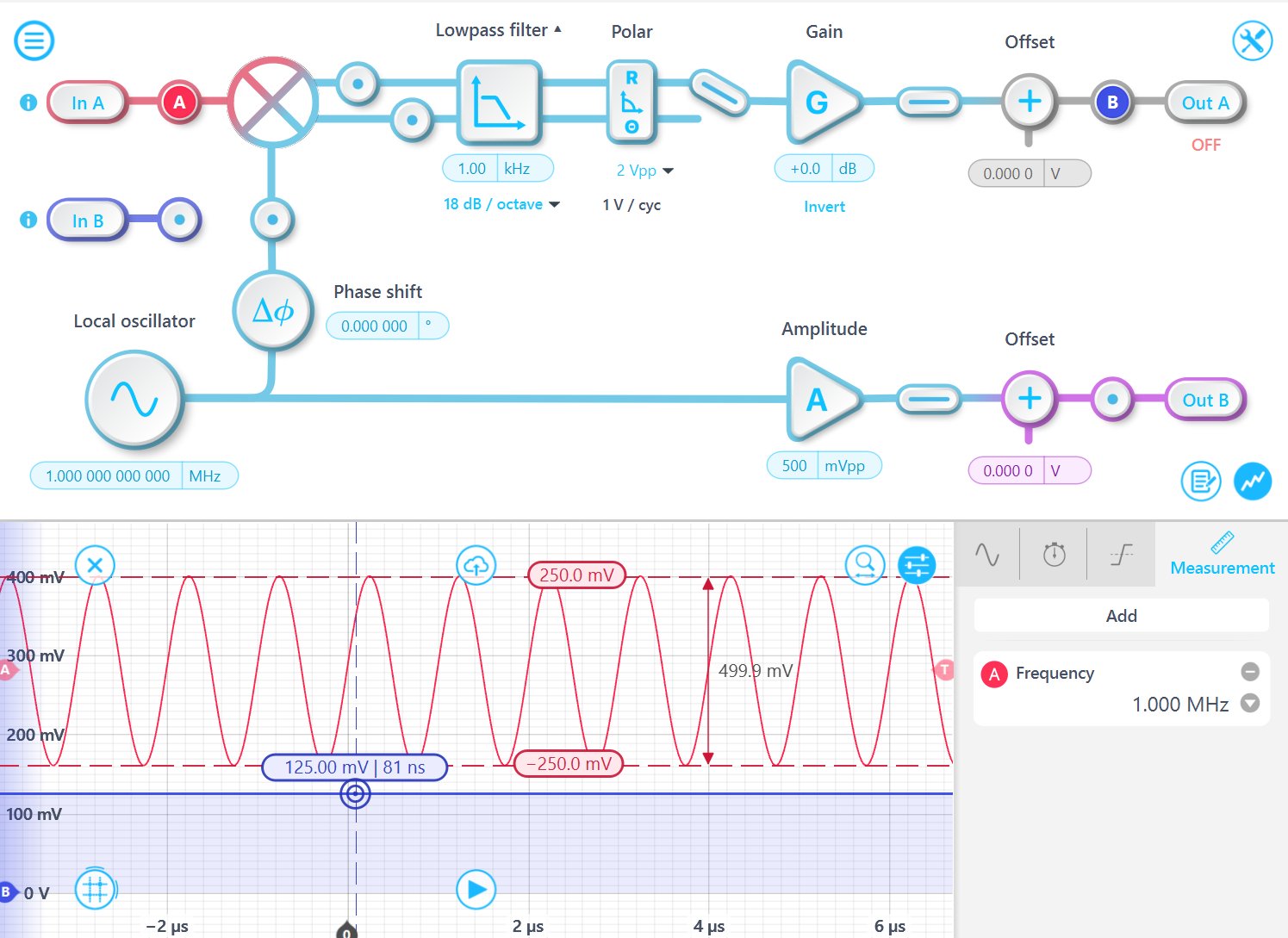
入力信号周波数は復調周波数と正確に一致する必要はありません。周波数差がローパス フィルタのコーナー周波数より小さければ、マッピング関係は有効です。

周波数f2で復調された入力信号A⋅sin(f1⋅t)の場合、混合後の結果の信号は、 A/2⋅{cos[(f1- f2)⋅t] - cos[(f1 + f2)⋅t]}です。ローパス フィルターを通過した後、高周波成分は減衰され、 A/2⋅cos[(f1- f2)⋅t]が残ります。Moku Mokuイン アンプはデュアル位相復調器 (同相および直交位相) を採用しているため、計算された振幅 R はsqrt({A/2⋅cos[(f1- f2)⋅t]}^2 + {A/2⋅sin[(f1- f2)⋅t]}^2) で、 A/2に等しくなります。

1 Vpp 振幅の 1 MHz 信号 10.000 を 10 MHz 復調信号を使用して復調します。出力は予想どおりの振幅を示し、100 Hz の周波数で周期的な位相変化を起こします。

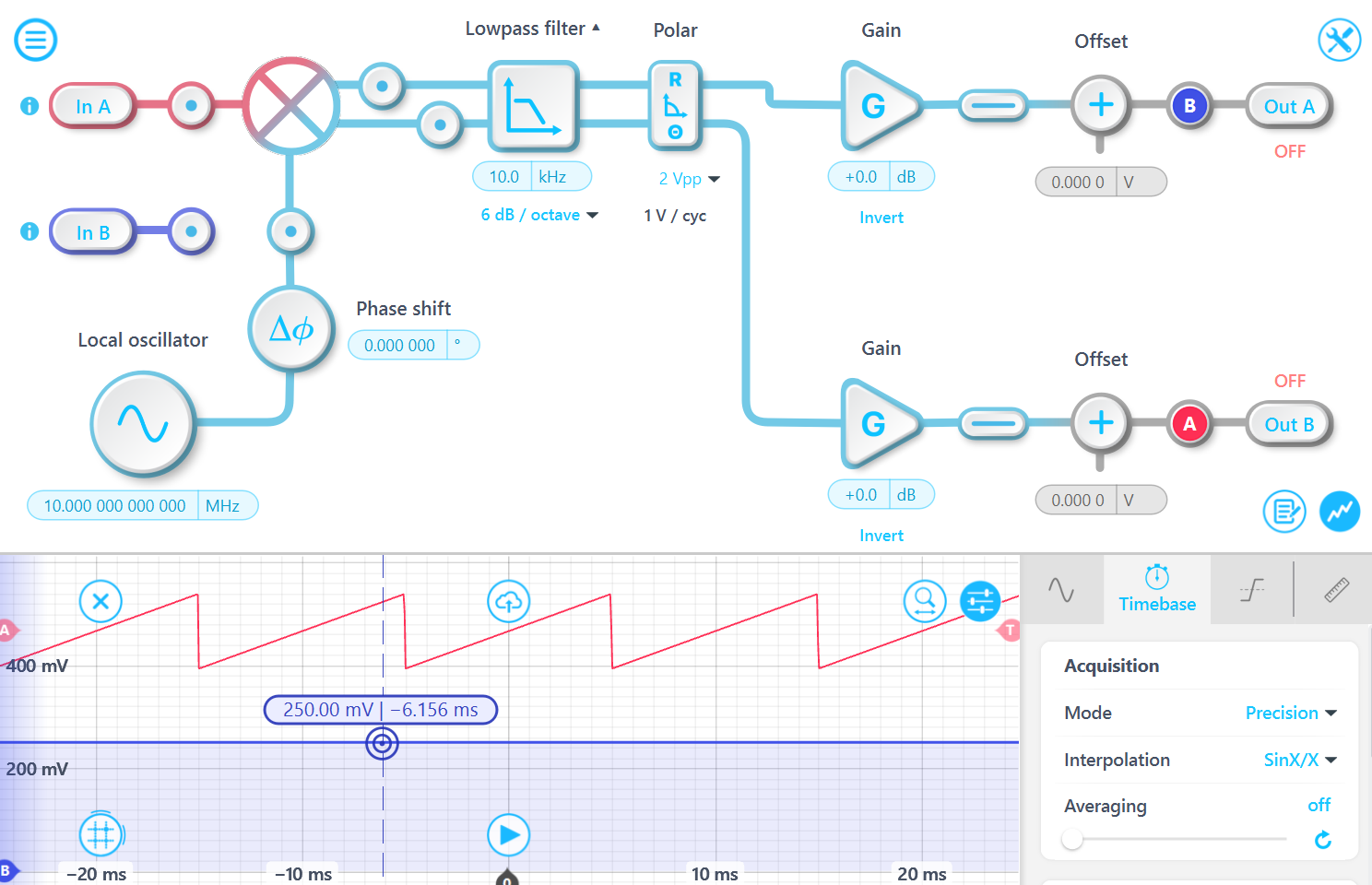
ただし、このマッピング関係は単一周波数トーン信号にのみ適用されることに注意してください。より複雑な信号の場合、追加の周波数成分がフィルタリングされ、信号損失と振幅減少が生じるため、この関係は成立しません。

たとえば、10 MHz と 1 MHz の 2 つの周波数トーンを含む入力信号を使用したテストを考えてみましょう。ベースライン信号は 1 MHz、500 mVpp の正弦波で、これに 10 MHz、500 mVpp の信号が重ねられています。この場合、合計入力信号振幅が 1 Vpp になったにもかかわらず、R 出力振幅は 125 mV のままです。これは、10 MHz トーンが 1 kHz 帯域幅のローパス フィルタによって除去されるためです。

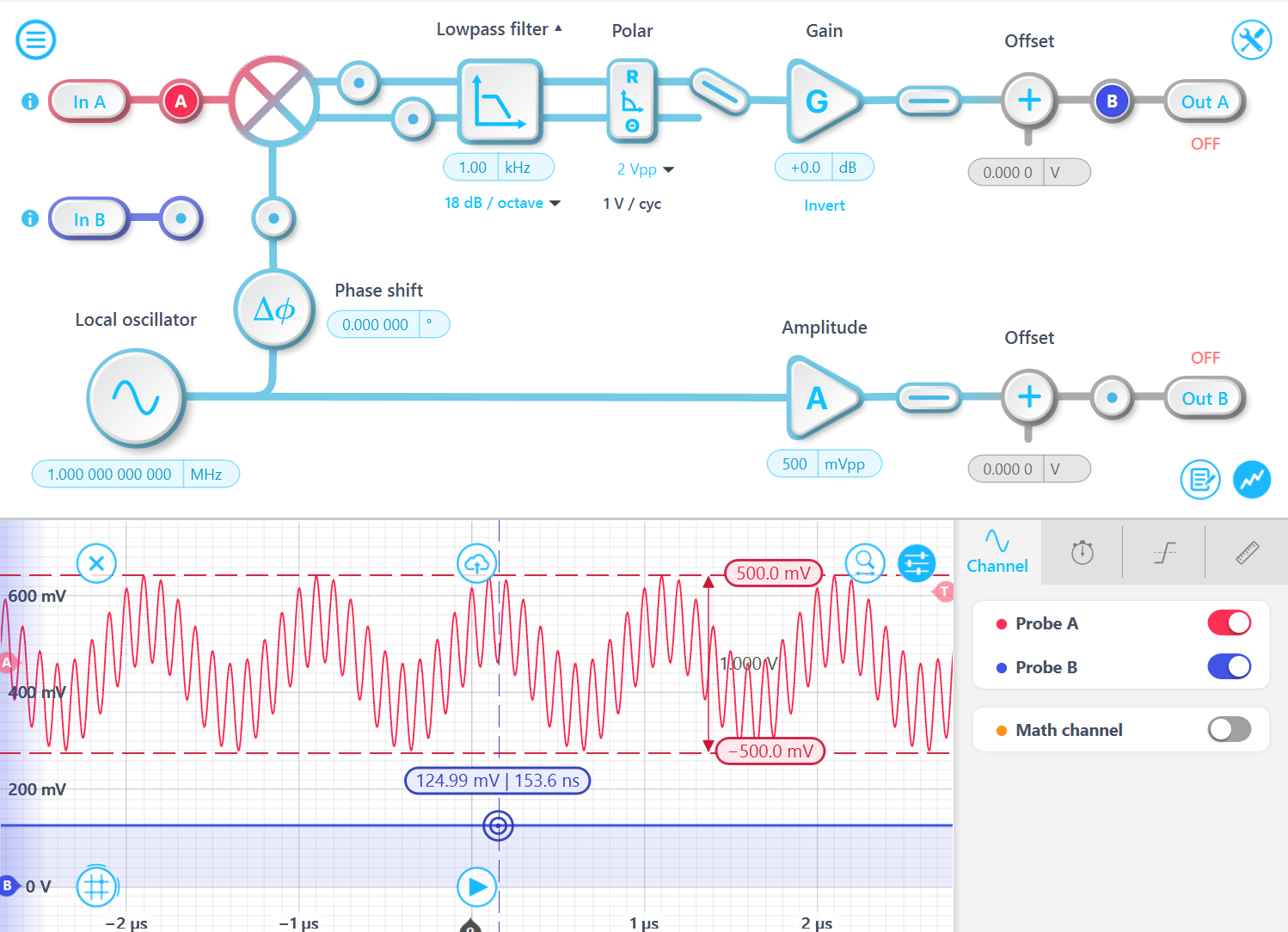
2. 振幅変調（AM）入力信号：

基本搬送波で変調されたメッセージ信号の場合、メッセージ周波数がローパス通過帯域内にある場合、復調振幅は元の変調信号のA⋅d/2​ になると予想されます。ここで、 Aは搬送波波形の振幅、 d は変調深度です。変調信号A⋅sin(f⋅t)⋅[1+d⋅sin(m⋅t)] は、復調後は(1−cos(2f⋅t))⋅A/2​⋅[1+d⋅sin(m⋅t)]と表すことができ、ローパス信号はA/2​⋅[1+d⋅sin(m⋅t)]です。

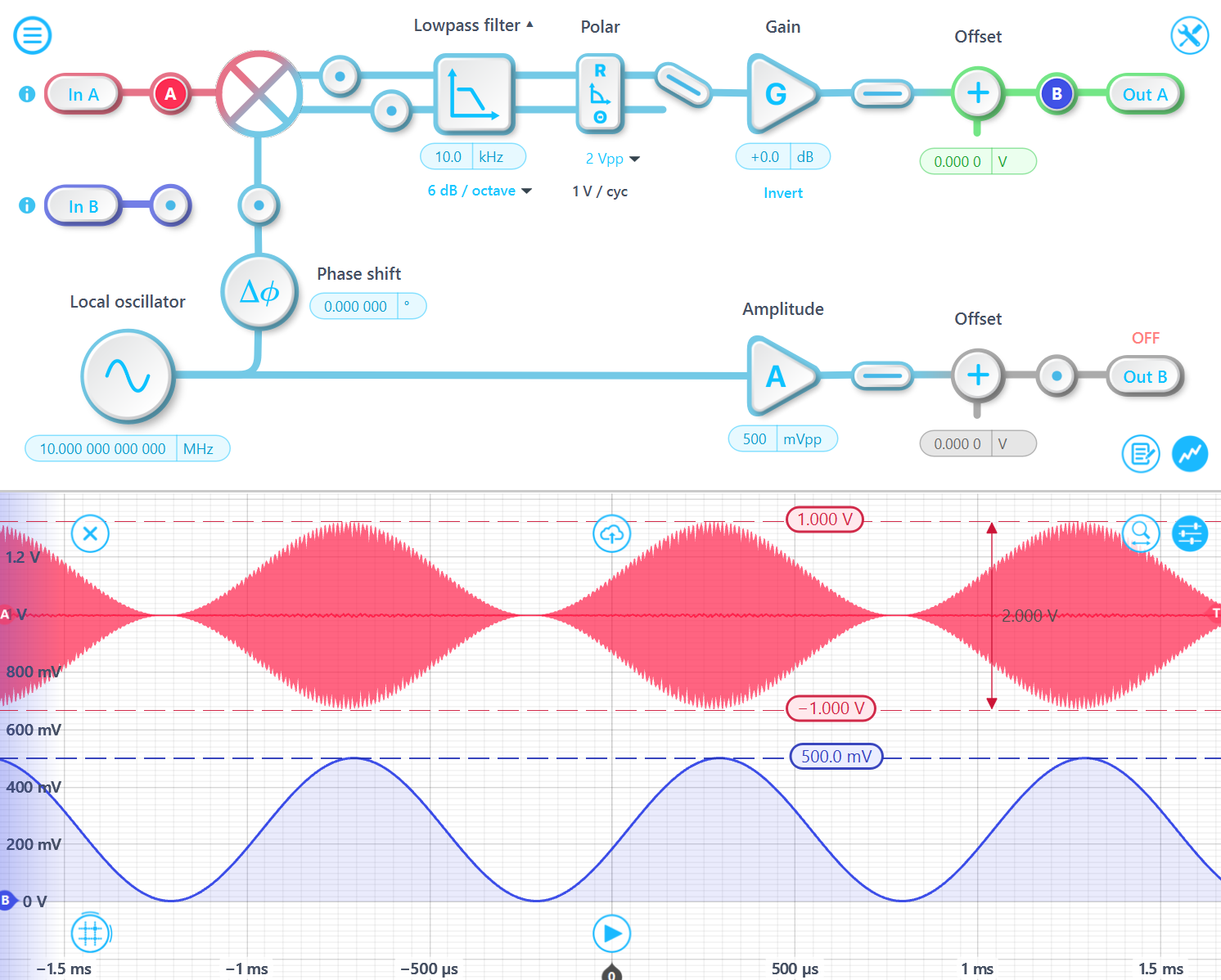
たとえば、1 Vpp 10 MHz 搬送波を持ち、1 kHz 正弦波で 100% 変調された入力信号を考えてみましょう。入力信号のピークツーピーク振幅は、A⋅sin(f⋅t)⋅[1+sin(m⋅t)]の最大値が 1 で、最小値が -1 であるため、2 Vpp です。復調された出力のピークツーピーク振幅は 500 mVpp で、 dが 100% であるため、1 Vpp の1/2 になります。

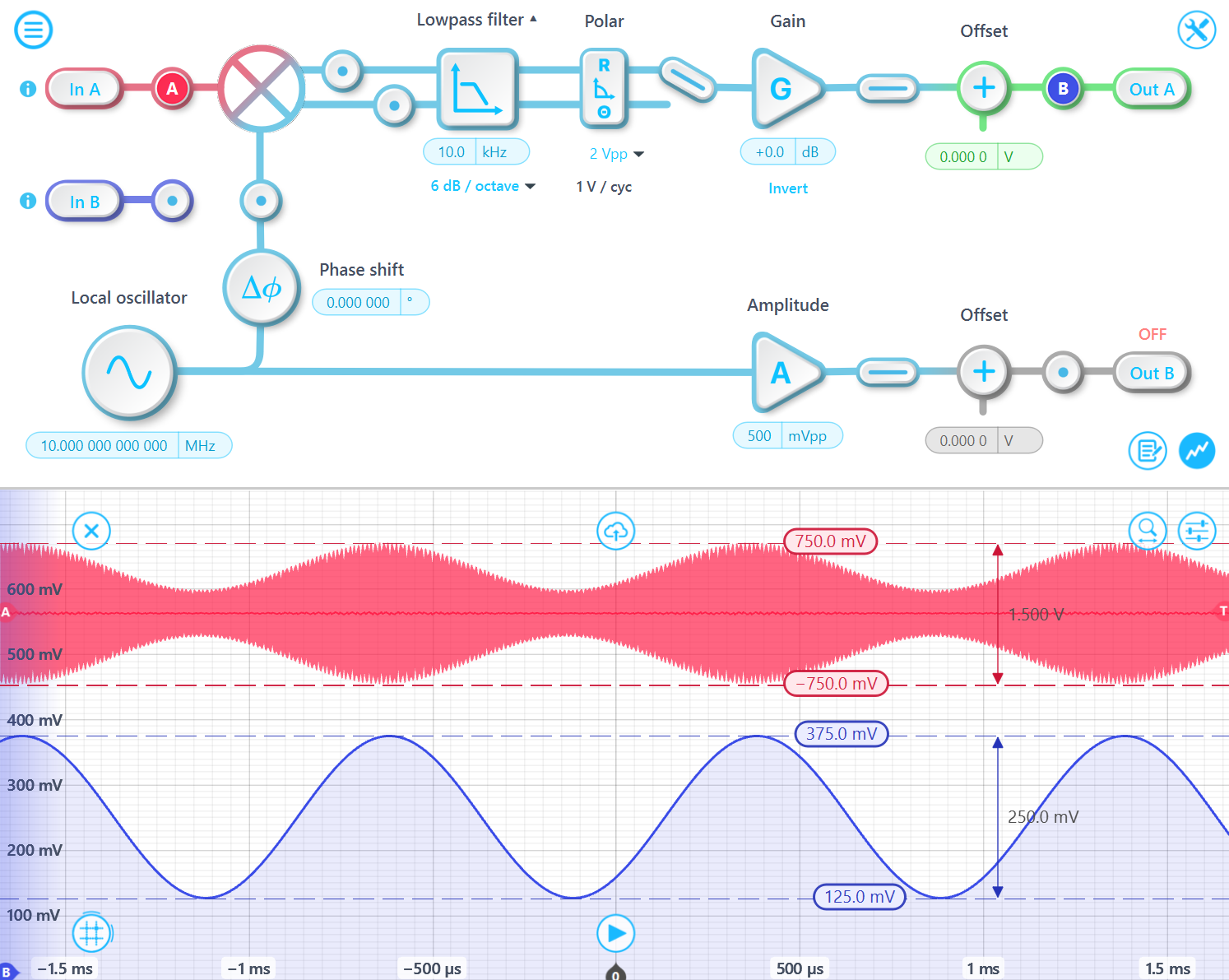
信号が50%変調されている場合、 A⋅sin(ft)⋅[1+0.5⋅sin(m⋅t)]の最大値は0.75、最小値は-0.75なので、入力信号のピークツーピーク振幅は1.5Vppです。また、復調された出力のピークツーピーク振幅は250mVppで、1Vppのd/2​です。

要約すると、入力と出力の振幅の関係は1/4マッピングに従います。ただし、これは信号が単一の周波数トーンで構成されている場合にのみ適用されます。言い換えると、R 出力は、復調周波数に一致する入力信号成分のピークツーピーク振幅の 4 分の 1 を表します。搬送波にメッセージ信号がある場合、復調されたメッセージ信号の振幅はA⋅d/2​ になります。ここで、 Aは搬送波振幅、 d は変調深度です。